计算几何小结:叉积
本文共 453 字,大约阅读时间需要 1 分钟。
一个神奇的东西,可以判断两线段是否相交,三点共线,多边形角形面积……
code:
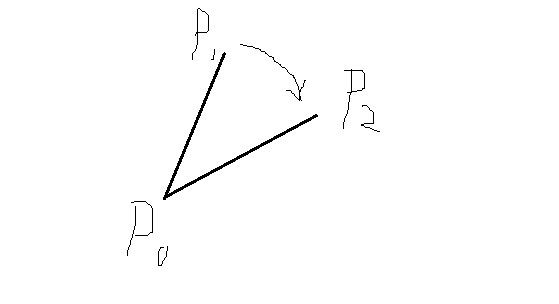
double multi(point p1,point p2,point p0){ double x1=p1.x-p0.x,x2=p2.x-p0.x; double y1=p1.y-p0.y,y2=p2.y-p0.y; return x1*y2-x2*y1;} 第一次看到简直一脸懵逼,什么鬼? 首先我们考虑p0是原点的情况。
当x1=x2时如果p1要顺时针旋转到p2,则他们的叉积小于0,否则大于0。
如果x1,x2变化,也容易证明,叉积依然小于0.
在其他象限也有这样的规律。
所以叉积的正负分别代表p1逆/顺时针得到p2
关于第三个参数p0,我感性的理解为以他为旋转中心。
那么问题来了,假如p1,p2,p0三点共线,那叉积是多少。
简单的猜想:0
why
我认为可以从叉积的几何意义理解。
叉积的绝对值除二就是那三个点组成的三角形的面积!
可以将图画出来,用割补法求,最后化简出来就是叉积的式子了。
你可能感兴趣的文章
ng build --aot --prod生成文件报错
查看>>
ng 指令的自定义、使用
查看>>
ng6.1 新特性:滚回到之前的位置
查看>>
nghttp3使用指南
查看>>
Nginx
查看>>
nginx + etcd 动态负载均衡实践(一)—— 组件介绍
查看>>
nginx + etcd 动态负载均衡实践(三)—— 基于nginx-upsync-module实现
查看>>
nginx + etcd 动态负载均衡实践(二)—— 组件安装
查看>>
nginx + etcd 动态负载均衡实践(四)—— 基于confd实现
查看>>
Nginx + Spring Boot 实现负载均衡
查看>>
Nginx + Tomcat + SpringBoot 部署项目
查看>>
Nginx + uWSGI + Flask + Vhost
查看>>
Nginx - Header详解
查看>>
Nginx - 反向代理、负载均衡、动静分离、底层原理(案例实战分析)
查看>>
Nginx - 反向代理与负载均衡
查看>>
nginx 1.24.0 安装nginx最新稳定版
查看>>
nginx 301 永久重定向
查看>>
nginx connect 模块安装以及配置
查看>>
nginx css,js合并插件,淘宝nginx合并js,css插件
查看>>
Nginx gateway集群和动态网关
查看>>